CRYPTOGRAPHIC AUTHENTICATION PROTOCOL ZERO-KNOWLEDGE SECRET ON ELLIPTIC CURVES USING PUBLIC KEYS AND RANDOM MESSAGES

Abstract

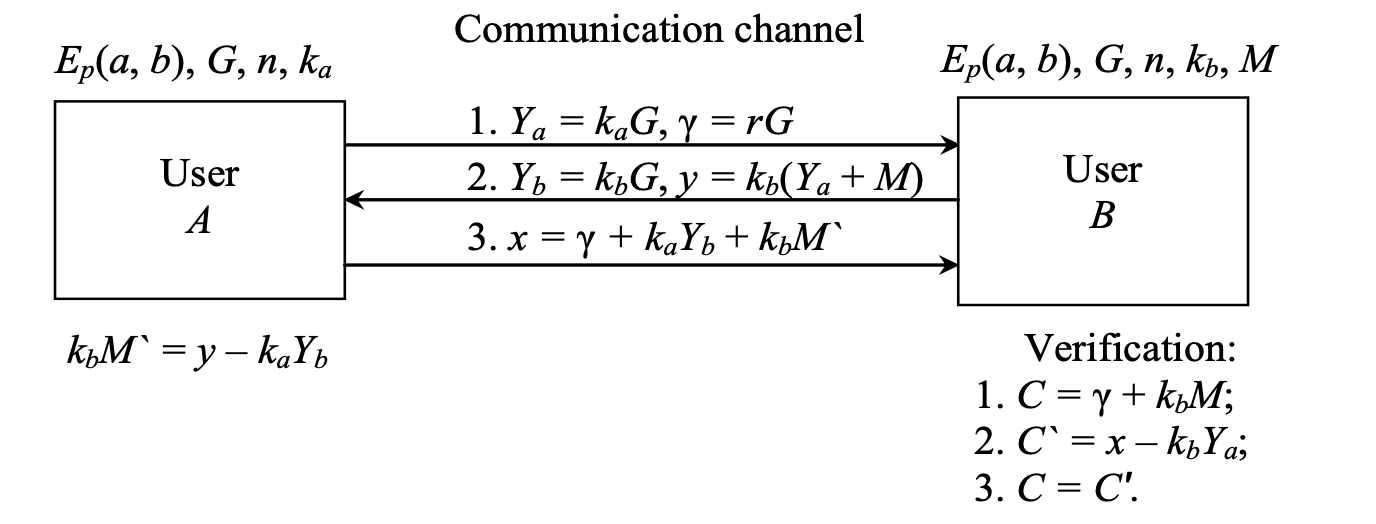
We propose a cryptographic protocol with zero-knowledge proof (ZKP) on elliptic curves (EC) using public keys and random messages, allowing to establish the truth of a statement not conveying any additional information about the statement itself. The cryptographic protocols based on zero-knowledge proof allow identification, key exchange and other cryptographic operations to be performed without leakage of sensitive information during the information exchange. The implementation of the cryptographic protocol of the zero-knowledge proof on the basis of the mathematical apparatus of elliptic curves allows to significantly reduce the size of the protocol parameters and increase its cryptographic strength (computational complexity of the breaking). The security of cryptosystems involving elliptic curves is based on the difficulty of solving the elliptic curve discrete logarithm problem. We determine the completeness and correctness of the protocol and give an example of the calculation is given. The cryptographic protocol was modeled in the High-Level Protocol Specification Language, the model validation and verification of the protocol were also performed. The software verification of the cryptographic protocol was performed using the software modules On the Fly Model Checker and Constraint Logic based Attack Searcher. In order to validate the cryptographic protocol resistance to intruder attacks, we used the Security Protocol Animator package for Automated Validation of Internet Security Protocols and Applications. The security of the proposed cryptographic protocol ZKP EC is based on the difficulty of solving the elliptic curve discrete logarithm problem). The recommended elliptical curves according to DSTU 4145-2002 may be used to implement such cryptographic protocol.